A harmadfokú Hermit-görbe kezdő és végpontjával és a kezdő és végpontban megadott érintőjével adott. Adott a p0 és p1 pont, valamint a t0 és t1 érintő vektor.

Keresünk egy olyan

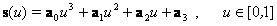
harmadfokú polinommal megadott görbét amelyre

teljesül, ahol a felső pont a derivált jele.

Ezek alapján az egyenletrendszer felírása és megoldása következik.

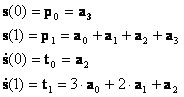
Az egyenletrendszer megoldása után

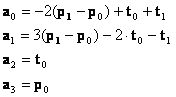
polinom-együtthatókat kapjuk. Ezeket visszahelyettesítve és átrendezve kapjuk:

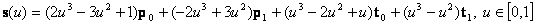
Az egyenletben szereplő együttható polinomokat Hermite-polinomoknak nevezzük, és a következőképpen jelöljük:

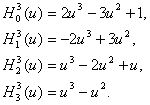
Ekkor a görbe felírható a Hermit-alappolinomok segítségével:

.

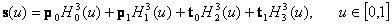Az előbbi összefüggést alapján az Hermit-görbét tekinthetjük úgy, mint a kontrolladatok (a p0 és p1 pont, valamint a t0 és t1) súlyozott összege.

Az egységesebb szemléletmód miatt felírhatjuk a görbét mátrix alakban is:

.

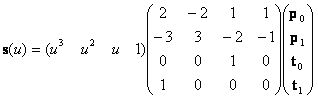Ha a végpontbeli érintőket egyre nagyobb mértékben növeljük, akkor kialakulhat hurok a görbén, azaz átmetszheti önmagát.