Sok feladat megoldásához az egydimenziós tömb struktúra már nem elegendő, vagy túl bonyolulttá tenné a kezelést. Ha például gyűjteni szeretnénk havonként és azon belül naponként a kiadásainkat. A kiadások számok, de a napokhoz rendelt indexek nehézkesek lennének, mert február 1-hez a 32-t, június 1-hez már a 152-es index tartozna. Egyszerűbb, ha a kiadásainkat két indexel azonosítjuk. Az egyik jelentheti a hónapot, a másik a napot. Ha már az évet is szeretnénk tárolni, akkor egy újabb index bevezetésére van szükségünk.

Nézzük meg egy egyszerű példán keresztül a deklarációt. Töltsünk fel egy 3x3 mátrixot véletlen számokkal és írassuk ki őket mátrix fromában a képernyőre.

static void Main(string[] args)

{

int[,] tm = new int[3,3];

int i, j ;

Random rnd = new Random();

for (i = 0; i < 3; i++)

{

for (j = 0; j < 3; j++)

{

tm[i,j] = rnd.Next(10,20);

Console.Write("{0} ",tm[i,j]);

}

Console.WriteLine();

}

Console.ReadLine();

}

Látható, hogy a deklarációkor a két indexet úgy jelezzük, hogy egy vesszőt teszünk a zárójelbe, majd a példányosításkor megadjuk az egyes indexekhez tartozó elemszámot.

A kétdimenziós tömböt feltölteni elemekkel, illetve kiíratni azokat elég két ciklus, ahol az egyik ciklusváltozó az egyik indextartományt futja végig, míg a másik ciklusváltozó a másik tartományt. Ha nem két, hanem többdimenziós tömböt használunk, akkor a ciklusok számma ennek megfelelúően fog nőni.

A példában látható, hogy a mátrix forma megtartás érdekében egyszerűen a sorok elemeit egymás mellé Write utasítás alkalmazásával írattuk ki. A belső ciklus minden sor kiírásáért felelős, így a sorok végén a soremelésről gondoskodtunk a WriteLine utasítással, melynek nem volt paramétere.

A kétdimenziós tömböt feltölthetjük kezdőértékkel, hasonlóan az egydimenziós esethez:

int[,] tm2 = new int[2,2] {{1,2},{3,4}};

Tekintsük a következő feladatot:

Töltsünk fel egy 3x3 mátrixot a billentyűzetről egész számokkal. Írassuk ki a szokásos formátumban, majd generáljuk a transzponáltját, és ezt is írassuk ki.

A szükséges tömb és ciklusváltozók deklarálása:

int[,] tm = new int[4,4];

int i, j ;

Töltsük fel a mátrixot billentyűzetről egész számokkal:

for (i = 0; i < 3; i++)

for (j = 0; j < 3; j++)

{

Console.Write("Kérem a {0}. sor {1}. oszlop elemét: ",i,j);

tm[i,j] = int.Parse(Console.ReadLine());

}

Írassuk ki a tömb elemeit mátrix formában:

Console.WriteLine("Az eredeti mátrix: ");

for (i = 0; i < 3; i++)

{

for (j = 0; j < 3; j++)

Console.Write("{0} ",tm[i,j]);

Console.WriteLine();

}

Ez futás közben így néz ki:

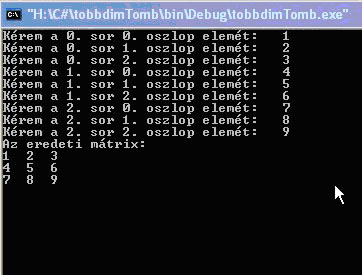
Deklaráljunk egy tr tömböt a transzponált mátrix elemeinek. Majd generáljuk le az eredeti tm tömbből. A transzponált mátrixot az eredeti mátrix sorainak és oszlopainak felcserélésével kapjuk.

int[,] tr = new int[3,3];

for (i = 0; i < 3; i++)

for (j = 0; j < 3; j++)

tr[i,j] = tm[j,i];

Újra ki kell íratni egy tömböt, most a transzponált mátrixot.

for (i = 0; i < 3; i++)

{

for (j = 0; j < 3; j++)

Console.Write("{0} ",tr[i,j]);

Console.WriteLine();

}

A program futtatását bemutató képernyő:

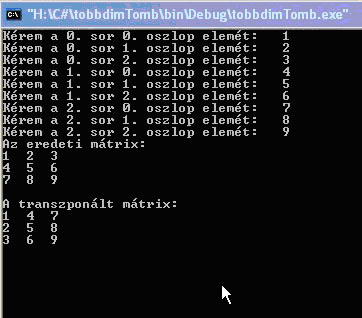
Vegyük észre, hogy a két kiíratásban csak a tömb neve a különböző. Feleslegesen írjuk le kétszer ugyanazt a kódot. Erre jobb megoldást ad az eljárásokról és függvényekről szóló fejezet.