|
Elektronikus Felsőoktatási Tankönyv- és Szakkönyvtár |
|
|
Elektronikus Felsőoktatási Tankönyv- és Szakkönyvtár |
A Bézier-görbe a kontrollpontjai affin transzformációjával szemben invariáns. Ez következik a de Casteljau-féle előállításból. Ezen tulajdonságot kihasználva, a görbe affin transzformációja (Pl.:eltolás, elforgatás, tükrözés, skálázás, párhuzamos vetítés) esetén elég a kontrollpontokra végrehajtani a transzformációt, mivel a transzformált pontok által meghatározott Bézier-görbe megegyezik az eredeti görbe transzformáltjával. De centrális vetítésre nézve nem invariáns.
Ha
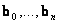
, akkor a Bezier görbe kontrollpontjainak konvex burkán belül van.
A Bézier-görbe kontrollpontjainak konvex burkán belül marad
A Bézier-görbe az első és utolsó kontrollponton áthalad.
A Bézier-görbe „szimmetrikus”, azaz 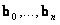a 
és a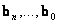 
pontok ugyanazt a görbét állítják elő.
Ha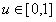 
akkor a Bézier-görbe kezdő- és végérintője:
.
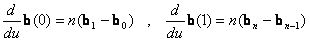Tehát a kezdő és a végpontban az érintők tartó egyenese a kontrollpoligon oldalai.
A Bézier-görbe és érintői
esetén az érintővektorok harmadát felmérve
A görbe globálisan változtatható, azaz, ha megváltoztatjuk egy kontrolpontjának a helyzetét, akkor az egész görbe alakváltozáson megy keresztül. Bebizonyítható a Bernstein-polinomok tulajdonsága alapján, hogy a
esetén a 
kontrollpontnak a
paraméterértéknél van legnagyobb hatása a görbe alakjára. Ez utóbbi tulajdonságot nevezik úgy, hogy a görbe pszeudolokálisan változtatható. Tehát a Bézier-görbe alakváltozása jól prognosztizálható.
A polinominális előállításból jól látható, hogy
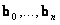
pontokat, azaz n+1 pontot n-edfokú görbével approximál, azaz a kontrollpontok számának növekedésével nő a poligon fokszáma is.