esetén a görbe Bernstein-polinom alakja:

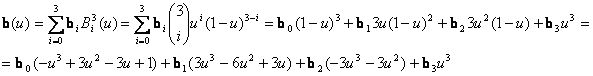
A görbe érintője:

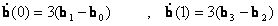
Ezután könnyedén megtalálhatjuk az Hermit-görbe és a Bézier-görbe közötti kapcsolatot. Ha az Hermit-görbe a p0 és p1 pontok, és a t0 és t1 érintőkkel van meghatározva, akkor a kezdő és végpontbeli érintőknek meg kell egyezniük a Bézier-görbe érintőivel, azaz 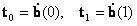, továbbá a kezdő és végpontok is egybeesnek.

Tehát az Hermit-göbével megegyező Bézier-görbe kontrollpontjai:

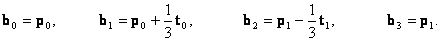
A harmadfokú Beziér-görbék (s természetesen az Hermit-görbék is) változatos képet mutathatnak.

Harmadfokú Bézier-görbék

Ha a harmadfokú Bézier-görbe kontrollpontjait nincsenek egy síkban, akkor a Bézier-görbe térgörbe lesz, azaz nem találunk olyan síkot amelyre a görbe minden pontja illeszkedne. A három kontrollpont esetén a másodfokú Bézier-görbe már egy jól ismert síkgörbe, parabola lesz.