Az előző fejezetben láttuk, hogyan milyen kapcsolat van az Hermit-görbe és a Bézier-görbe között. Ha több mint két pontot szeretnénk összekötni interpoláló görbével, akkor kézenfekvő megoldás a kapcsolódó harmadfokú Bézier-görbék alkalmazása, amelyek természetesen Hermit-görbék is lehetnek. Kapcsolódó görbeívek használata igen gyakori a modellezésben. Ilyen esetekben a csatlakozásnál megadjuk a folytonosság mértékét. Ha az 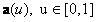és 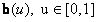két csatlakozó görbe amely négy négy kontrollponttal adott: a0,a1,a2,a3 és b0,b1,b2,b3.

A kapcsolódásnál megkövetelhetünk nulladrendű C0, elsőrendű C1, illetve másodrendű C2 folytonosságot. Általánosságban azt mondhatjuk, hogy két csatlakozógörbe kapcsolódása Cn folytonos, ha az egyik görbe deriváltjai a végpontjában megegyeznek a másik görbe deriváltjaival a kezdőpontban, az n. deriváltig bezárólag. A matematikai folytonosság vagy parametrikus folytonosság mellett létezik geometriai folytonosság is. Pl. G0 megegyezik C0-lal, és G1 folytonosan kapcsolódik két görbe, ha az érintők a kapcsolódási pontban egy irányba néznek, de a hosszuk nem feltétlenül egyezik meg, azaz egyik érintő skalárszorosa a másiknak: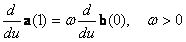

A nulladrendű folytonossághoz elegendő, ha a csatlakozáskor keletkező görbe megrajzolható anélkül, hogy a ceruzánkat felemelnénk. A mi esetünkben ez akkor teljesül, ha az első görbe végpontja megegyezik a második görbe kezdőpontjával, azaz: 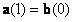és mivel ezen görbepontok megegyeznek a megfelelő kontrollpontokkal, hiszen a Bézier-görbe a végpontokat interpolálja, ezért a3 = b0 kell, hogy teljesüljön.

Az elsőrendű, C1 folytonossághoz az érintőknek kell megegyezniük, azaz 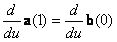kell, hogy teljesüljön. Ez a kontrollpontokra az (a3 - a2) = (b1 - b0) feltételt jelenti, azaz, amellett, hogy a két szegmens kezdő- és végpontja megegyezik, az a2, a3=b0, b1 pontoknak egy egyenesre kell illeszkedniük és az a3 pontnak feleznie kell az a2b1 szakaszt.

A másodrendben folytonos kapcsolódáshoz a fenti feltételeken kívül a következőnek kell teljesülnie: 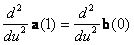Ez a kontrollpontokra nézve a következőt jelenti:

((a3 - a2) - (a2 - a1)) = ((b2 - b1) - (b1 - b0))

ami geometriai szempontból azt jelenti, hogy az a1a2 egyenes és a b1b2 egyenes m metszéspontjára teljesül, hogy a2 felezi az a1m szakaszt, b1 pedig felezi az mb2 szakaszt.

A gyakorlatban C2 folytonosságú kapcsolat elégséges, pl. animáció esetén a mozgó kamera által készített felvétel akkor lesz valósághű, ha a második derivált is megegyezik. Gondoljunk arra, hogy az út/idő függvény második deriváltja a gyorsulást adja, tehát ha a kapcsolódási pontban megváltozik a gyorsulás, akkor szaggatott felvételt kapunk.

C0, C1 és C2 folytonosan kapcsolódó Bézier-görbék