A cardinal spline egy a kontrollpontokat interpoláló, azaz az előre megadott pontokon adott sorrendben áthaladó görbe, tulajdonképpen elsőrendben folytonosan csatlakozó harmadfokú (kubikus) Hermit-görbék sorozata. Mivel az előző fejezetben már kimutattuk a Hermit- és a Bézier-görbe közötti kapcsolatot, ezért a cardinal spline megadhatjuk harmadfokú C1 folytonosan kapcsolódó Bézier-görbék sorozataként is. Járjunk el az utóbbi módon!

3 pontot interpoláló C1 folytonosan csatlakozó Bézier-görbék

Az i. Bézier szegmens kezdő és végpontja a szomszédos a pi és pi+1 pontok. A görbe deriváltja egy közbülső pi pontban párhuzamos pi-1 pi+1 egyenessel, azaz

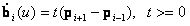
Ne felejtsük el, hogy a harmadrendű Bézier-görbe négy pontjával (négy vektorral) adott, pl. négy kontrollpont, vagy ha Hermit-görbeként adjuk meg, akkor a kezdő és a vég pont, valamint a kezdő és a végpontban az érintők. Az i. Bézier szegmens kezdő és végpontja 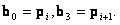 Mivel a görbe érintője:

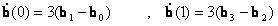
ezért minden kontrollpont minden szegmens esetén most már meghatározható. Az érintők meghatározásánál használhatunk egy tenziós értéket, amely az érintők nagyságát befolyásolja. Ha akkor a Catmul-Rom spline-t, ha akkor a kontrollpontokat összekötő poligont kapjuk meg.

A t tenziós érték hatása a görbe alakjára

Zárt görbe estén az érintő a kezdő és a végpontban is az 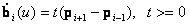általános képlettel határozható meg.

Zárt görbék különböző t értékeknél

Az előbbi képeket előállító program részlet:

private void Form1_Paint(object sender, System.Windows.Forms.PaintEventArgs e)

{

Pen redPen = new Pen(Color.Red, 4);

Color myColor = new Color();

FillMode myFill=new FillMode();

// Pontok megadása

PointF point1 = new PointF(100.0F, 350.0F);

PointF point2 = new PointF(250.0F, 150.0F);

PointF point3 = new PointF(430.0F, 170.0F);

PointF point4 = new PointF(550.0F, 400.0F);

PointF[] curvePoints ={

point1,

point2,

point3,

point4,

};

// Kontrolpoligon megrajzolása:

e.Graphics.DrawLines(redPen, curvePoints);

// Cardinal-spline kirajzolása változó tenziós értékkel:

for (float i = 0.0F; i <= 2; i+=0.5F)

{float tension = i*1.0F;

myColor=Color.FromArgb((int)(i*63.0F),(int)(i*63.0F),(int)(i*63.0F));

e.Graphics.DrawCurve(new Pen(myColor,2), curvePoints,tension);

// Zárt görbe előállítása:

e.Graphics.DrawClosedCurve(new Pen(Color.Red,2), curvePoints,tension,myFill);

}

}

Ahogy a fenti programrészletből láthattuk, hogy GDI+ segítségével lehetőségünk van cardinal spline előállítására DrawCurve metódussal. Mivel a GDI+ kihasználja, hogy a cardinal spline csatlakozó Bézier-görbékből áll, ezért szükség van egy Bézier-görbét előállító metódusra is. A DrawBezier négy kontroll pontra illeszt közelítő görbét, míg a DrawBeziers pedig C0 folytonosan kapcsolódó Bézier-görbéket rajzol.

7 pont esetén a DrawBeziers metódus futási eredménye