”Ismétlés a tudás anyja”.

Hernyák Zoltán

Az eddig megírt programok szekvenciális működésűek voltak. A program végrehajtása elkezdődött a Main függvény első utasításán, majd haladtunk a másodikra, harmadikra, stb… amíg el nem értük az utolsó utasítást, amikor is a program működése leállt.

Nem minden probléma oldható meg ilyen egyszerűen. Sőt, leggyakrabban nem írható fel a megoldás ilyen egyszerű lépésekből. Vegyük az alábbi programozási feladatot: írjuk ki az első 5 négyzetszámot a képernyőre (négyzetszámnak nevezzük azokat a számokat, amelyek valamely más szám négyzeteként előállíthatóak - ilyen pl. a 25).

public void Main()

{

Console.WriteLine(”1. négyzetszám = 1”);

Console.WriteLine(”2. négyzetszám = 4”);

Console.WriteLine(”3. négyzetszám = 9”);

Console.WriteLine(”4. négyzetszám = 16”);

Console.WriteLine(”5. négyzetszám = 25”);

}

A fenti program még a hagyományos szekvenciális működés betartásával íródott. De képzeljük el ugyanezt a programot, ha nem az első 5, de első 50 négyzetszámot kell kiírni a képernyőre!

Vegyük észre, hogy a program sorai nagyjából egyformák, két ponton különböznek egymástól: hogy hányadik négyzetszámról van szó, és annak mennyi az értéke. Az hogy hányadik négyzetszámról van szó – az mindig 1-gyel nagyobb az előző értéktől.

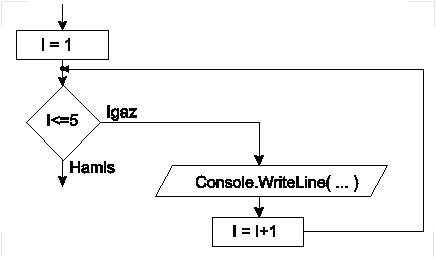
Nézzük az alábbi pszeudó-utasítássorozatot:

1. I := 1// az I változó értéke legyen ’1’

2. Írd ki: I,”. négyzetszám = ”, I*I

3. I := I+1 // az I változó értéke növelve 1-el

4. ugorj újra a 2. sorra

Ennek során kiíródik a képernyőre az „1. négyzetszám= 1”, majd a „2. négyzetszám = 4”, „3. négyzetszám = 9”, stb…

A fenti kódot nevezhetjük kezdetleges ciklusnak is. A ciklusok olyan programvezérlési szerkezetek, ahol a program bizonyos szakaszát (sorait) többször is végrehajthatjuk. Ezt a szakaszt ciklus magnak nevezzük.

A fenti példaprogramban ez a szakasz (a ciklusmag) a 2. és a 3. sorból áll. A 4. sor lényege, hogy visszaugrik a ciklusmag első utasítására, ezzel kényszerítve a számítógépet a ciklusmag újbóli végrehajtására.

Vegyük észre, hogy ez a ciklus végtelen ciklus lesz, hiszen minden egyes alkalommal a 4. sor elérésekor visszaugrunk a 2. sorra, így a program a végtelenségig fut. Ez jellemzően helytelen viselkedés, az algoritmusok, és a programok egyik fontos viselkedési jellemzője, hogy véges sok lépés végrehajtása után leállnak. Módosítsunk a kódon:

1. I := 1// az I változó legyen ’1’

2. Ha az I értéke nagyobb, mint 5, akkor ugorj a 6. sorra

3. Írd ki: I,”. négyzetszám = ”, I*I

4. I := I+1 // az I változó értéke növelve 1-el

5. ugorj újra a 2. sorra

6. ….

A 2. sorba egy feltétel került, mely ha teljesül, akkor befejezzük a ciklusmag végrehajtását, mivel ’kilépünk’ a ciklusból, a ciklus utáni első utasításra ugorva.

Hogy ezen feltétel legelső alkalommal is kiértékelhető legyen, az 1. sorban beállítjuk az I változó értékét (értékadás). Valamint szintén figyeljük meg a 4. sort. Ezen sor is nagyon fontos, hiszen az I értéke e nélkül nem érhetné el a kilépéshez szükséges 6 értéket.

A ciklusoknak tehát az alábbi fontos jellemzőjük van:

A C#-ban a legnépszerűbb ciklus a FOR ciklus:

public void Main()

{

int i;

for (i=1;i<=5;i=i+1)

{

Console.WriteLine(”{0}. négyzetszám = {1}”,i,i*i);

}

}

A fenti példában a for kulcsszóval jelöljük, hogy ciklus szeretnénk írni. A for kulcsszó után zárójelben három dolgot kell megadni:

Formailag a három részt pontosvesszővel kell elválasztani. A ciklusmagot pedig kapcsos zárójelek közé kell tenni (utasításblokk). A C# az alábbi módon értelmezi a for ciklust:

Ha a vezérlő feltétel igaz, akkor végrehajtja a ciklusmag utasításait, ezért ebben az esetben a vezérlő feltételt a ciklusban maradás feltételének is nevezhetjük.

Másik dolog, amit megfigyelhetünk: a vezérlő feltétel kiértékelése már legelső alkalommal is a ciklusmag előtt hajtódik végre. Ennek megfelelően egy hibás kezdőértékadás eredményezheti azt is, hogy a ciklusmag egyetlen egyszer sem hajtódik végre. Például:

for (i=10;i<=5;i=i+1)

{

Console.WriteLine(i);

}

A ’for’ ciklusra jellemző, hogy tartozik hozzá egy ciklusváltozó, melyet az esetek többségében ’i’-vel jelölünk, elsősorban hagyománytiszteletből. Ezen i változó felveszi a kezdőértékét, majd szintén az esetek többségében ezt az értéket minden ciklusmag lefutása után 1-el növeli, amíg túl nem lépjük a végértéket. A for ciklus egy nagyon gyakori alakja tehát felírható az alábbi módon (’cv’ jelöli a ciklusváltozót):

for (cv = kezdőérték, cv <= végérték, cv = cv+1) ...

Ennek megfelelően előre kiszámítható, hogy a ciklusmag hányszor hajtódik végre:

for (i=1;i<=10;i++)

{

Console.WriteLine(i);

}

Ezen ciklus magja legelső alkalommal az i=1, majd i=2, …, i=10 értékekre hajtódik végre, összesen 10 alkalommal.

Vegyük az alábbi programozási feladatot: kérjünk be 3 számot, és írjuk ki a képernyőre a 3 szám összegét. Az első megoldás még nem tartalmaz ciklust:

int a,b,c,ossz;

a = Int32.Parse( Console.ReadLine() );

b = Int32.Parse( Console.ReadLine() );

c = Int32.Parse( Console.ReadLine() );

ossz = a+b+c;

Console.WriteLine(”A számok összege ={0}”,ossz);

Ugyanakkor, ha nem 3, hanem 30 számról lenne szó, akkor már célszerűtlen lenne a program ezen formája. Kicsit alakítsuk át a fenti programot:

int a,ossz;

ossz = 0;

a = Int32.Parse( Console.ReadLine() );

ossz = ossz+a;

a = Int32.Parse( Console.ReadLine() );

ossz = ossz+a;

a = Int32.Parse( Console.ReadLine() );

ossz = ossz+a;

Console.WriteLine(”A számok összege ={0}”,ossz);

A fenti program ugyanazt teszi, mint az előző, de már látszik, melyik az utasításcsoport, amelyet 3-szor meg kell ismételni. Ebből már könnyű ciklust írni:

int i,a,ossz=0;

for(i=1;i<=3;i=i+1)

{

a = Int32.Parse( Console.ReadLine() );

ossz = ossz+a;

}

Console.WriteLine(”A számok összege ={0}”,ossz);

Sokszor ez a legnehezebb lépés, hogy egy már meglévő szekvenciális szerkezetű programban találjuk meg az ismételhető lépéseket, és alakítsuk át ciklusos szerkezetűvé.

Programozási feladat: Készítsük el az első 100 egész szám összegét.

int i,ossz=0;

for (i=1; i<=100 ; i=i+1)

{

ossz = ossz + i;

}

Console.WriteLine(”Az első 100 egész szám összege ={0}”,ossz);

Jegyezzük meg, hogy a ciklusokban az i=i+1 utasítás nagyon gyakori, mint léptető utasítás. Ezt gyakran i++ alakban írják a programozók. A ++ egy operátor, jelentése ’növeld meg 1-gyel az értékét’. A párja a -- operátor, amelynek jelentése: ’csökkentsd 1-gyel az értékét’.

Másik észrevételünk, hogy aránylag gyakori, hogy a ciklusmag egyetlen utasításból áll csak. Ekkor a C# megengedi, hogy ne tegyük ki a blokk kezdet és blokk vége jeleket. Ezért a fenti kis program az alábbi módon is felírható:

int i,ossz=0;

for (i=1; i<=100 ; i++ )

ossz = ossz + i;

Console.WriteLine(”Az első 100 egész szám összege ={0}”,ossz);

Magyarázat: a program minden lépésben hozzáad egy számot az ’ossz’ változóhoz, amelynek induláskor 0 a kezdőértéke. Első lépésben 1-et, majd 2-t, majd 3-t, …, majd 100-t ad az ossz változó aktuális értékéhez, így állítván elő az első 100 szám összegét.

Megjegyzés: a fenti feladat ezen megoldása, és az alkalmazott módszer érdekes tanulságokat tartalmaz. Ugyanakkor a probléma megoldása az első N négyzetszám összegképletének ismeretében egyetlen értékadással is megoldható:

ossz= 100*101 / 2;

Programozási feladat: Határozzuk meg egy szám faktoriálisának értékét. A számot kérjük be billentyűzetről.

int szam,i,fakt=1;

szam = Int32.Parse( Console.ReadLine() );

for (i=1; i<=szam ; i++ )

fakt = fakt * i;

Console.WriteLine(”A(z) {0} szám faktoriálisa = {1}”, szam, fakt );

Magyarázat: pl. a 6 faktoriális úgy számolható ki, hogy 1*2*3*4*5*6. A program a ’fakt’ változó értékét megszorozza először 1-el, majd 2-vel, majd 3-al, …, végül magával a számmal, így számolva ki lépésről lépésre a végeredményt.

Megjegyzés: a ’szam’ növelésével a faktoriális értéke gyorsan nő, ezért csak kis számokra (kb. 15-ig) tesztelhetjük csak a fenti programot.

Programozási feladat: Határozzuk meg egy szám pozitív egész kitevőjű hatványát! A számot, és a kitevőt kérjük be billentyűzetről!

int szam,kitevo,i,ertek=1;

szam = Int32.Parse( Console.ReadLine() );

kitevo = Int32.Parse( Console.ReadLine() );

for (i=1; i<=kitevo ; i++ )

ertek = ertek * szam;

Console.WriteLine(”A(z) {0} szám {1}. hatványa = {2}”,

szam,kitevo,ertek);

Magyarázat: pl. 4 harmadik hatványa kiszámolható úgy, hogy 4*4*4. A program a ’ertek’ változó értékét megszorozza annyiszor a ’szam’-al, ahányszor azt a kitevő előírja.

Programozási feladat: Határozzuk meg egy szám osztóinak számát! A számot kérjük be billentyűzetről!

int szam,i,db=0;

szam = Int32.Parse( Console.ReadLine() );

for (i=1; i<=szam ; i++ )

if (szam%i==0) db++;

Console.WriteLine(”A(z) {0} szám osztóinak száma: {1}.”,szam,db);

Magyarázat: a 10 lehetséges osztói az 1..10 tartományba esnek. A módszer lényege, hogy sorba próbálkozunk a szóba jöhető számokkal, mindegyiket ellenőrizve, hogy az osztója-e a számnak, vagy sem. Az oszthatóságot a ’%’ operátorral ellenőrizzük. A % operátor meghatározza a két operandusának osztási maradékát (pl. a 14%4 értéke 2 lesz, mert 14 osztva 4-gyel 2 osztási maradékot ad). Amennyiben az osztási maradék 0, úgy az ’i’ maradék nélkül osztja a ’szam’ változó értékét, ezért az ’i’ változóban lévő érték egy osztó. Minden osztó-találat esetén növeljük 1-gyel a ’db’ változó értékét.

Programozási feladat: Írassuk ki a képernyőre egy szám összes többszörösét, amelyek nem nagyobbak, mint 100, csökkenő sorrendben! A számot kérjük be billentyűzetről!

int szam,i;

szam = Int32.Parse( Console.ReadLine() );

for (i=100; i>=szam ; i-- )

if (i % szam == 0) Console.WriteLine(”{0} ”,i);

Magyarázat: elindulunk 100-tól, visszafele haladunk, minden lépésben csökkentve a ciklusváltozónk értékét (i--). Minden lépésben megvizsgáljuk, hogy a szóban forgó ’i’ többszöröse-e az eredeti számnak. Ez akkor teljesül, ha a szám maradék nélkül osztja az ’i’-t. Valahányszor találunk ilyen ’i’ értéket, mindannyiszor kiírjuk azt a képernyőre.

Ugyanezen feladat megoldható hatékonyabban, ha figyelembe vesszük, hogy ezen számok egymástól ’szam’ távolságra vannak:

int szam,i,max;

szam = Int32.Parse( Console.ReadLine() );

max = (100/szam)*szam;

for (i=max; i>=szam ; i=i-szam )

if (i % szam == 0) Console.WriteLine(”{0} ”,i);

Magyarázat: a ’100/szam’ osztási művelet, mivel két egész szám típusú érték között kerül végrehajtásra automatikusan egész osztásnak minősül. Ha a ’szam’ értéke pl. 7, akkor a ’100/szam’ eredménye 14. Ha ezt visszaszorozzuk a ’szam’-al, akkor megkapjuk a legnagyobb olyan értéket, amely biztosan többszöröse a ’szam’-nak, és nem nagyobb mint 100, és a legnagyobb ilyen többszöröse a ’szam’-nak, amely nem nagyobb mint 100 (’max’). Ez lesz a kiinduló értéke a ciklusváltozónak. A további többszörösöket úgy kapjuk, hogy a kiinduló értéket minden cikluslépésben csökkentjük ’szam’-al.